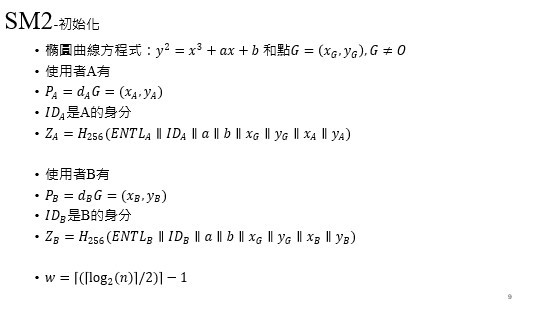SM2為橢圓曲線的公開密碼算法，其中橢圓曲線分為：
F_p上的橢圓曲線
F_p(p是大於3的質數)上的橢圓曲線方程式：
y^2=x^3+ax+b, a,b∈F_p並且 (4a^3+27b^2 )mod p≠0

F_(2^m ) 上的橢圓曲線
F_(2^m )上的橢圓曲線方程式：
y^2+xy=x^3+ax^2+b, a,b∈F_(2^m ) 且 b≠0

橢圓曲線的公鑰是一個點(x,y)，私鑰是一個數值。而基點G配上私鑰的數值就能生成公鑰，算法是公鑰=G+G+…+G共私鑰的數值次。

一開始會先初始化，這邊我們用F_p的橢圓曲線方程式：y^2=x^3+ax+b 和點G=(x_G,y_G ), G≠O，其中H代表雜湊。

使用者A有自己的公鑰P_A和自己的私鑰d_A，算法是P_A=d_A G=(x_A,y_A)
ID_A是A的身分，Z_A=H(ENTL_A∥ID_A∥a∥b∥x_G∥y_G∥x_A∥y_A)，ENTL_A是ID的長度再轉換為2位元組的。

使用者B有自己的公鑰P_B和自己的私鑰d_B，算法是P_B=d_B G=(x_B,y_B)
ID_B是B的身分，Z_B=H_256 (ENTL_B∥ID_B∥a∥b∥x_G∥y_G∥x_B∥y_B)，ENTLB是ID的長度再轉換為2位元組的。
ZA和ZB是金鑰交換和簽章才會用到，裡面會包含ID、橢圓曲線的點、基點和自己公鑰。

初始化完就能做加密、解密、金鑰交換和簽章。 可以參考以下圖片!